728x90
그리디 알고리즘(Greedy algorithm) - 탐욕법
- 가장 직관적인 형태의 알고리즘이며, 눈 앞에 보이는 최적의 상황만을 쫓는 알고리즘이다.
- 항상 최적의 결과를 뽑지는 못하지만, 확률 상 최적의 결과에 근사한 값을 빠르게 구할 수 있다.
- 즉, 특정한 상황에서 최적의 해를 보장하는 극한의 효율충 알고리즘
- 효율충인만큼 자원에 접근할 때 무조건 큰 경우, 긴 경우 등의 조건으로 문제를 극단적으로 접근하기 때문에 정렬 기법이 함께 사용되는 경우가 많다.
- 예시는 크루스칼 알고리즘으로 '모든 간선을 정렬한 이후에 짧은 간선으로 연결하는' 최소 신장 트리 알고리즘이 있다.
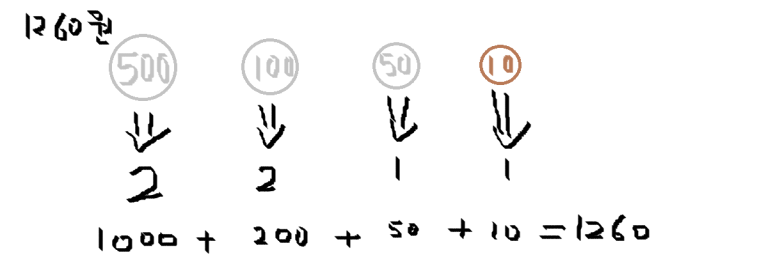
- 예시 문제로 일정 금액을 동전을 사용하여 낼 때 최소한의 개수로 낼 수 있는지 확인하는 문제
import sys
# 금액을 입력받고
n = int(input())
# 동전이 최소 몇 개인지 카운트
count = 0
# 동전 종류를 배열에 넣고
coins = [500, 100, 50, 10]
# 배열에서 동전값을 하나씩 돌리면서
for coin in coins:
# 전체 금액에서 금액이 큰 동전 순으로 몫을 카운트에 넣고
count += n // coin
# 전체 금액값에 나머지를 넣는다.
# 이러면 각 동전으로 나올 수 있는 값을 다 빼고 남은 금액만 남게되어
# 다음 동전으로 또 나뉘어 떨어진다.
n = n % coin
print(count)- 소비 금액이 1260원이라고 가정했을 때, 500원 2개, 100원 2개, 50원 1개, 10원 1개 해서 1260원. 총 6개의 동전을 사용해 최소 개수로 구할 수 있다.
- 가장 큰 화폐부터 거슬러 주는 것이 최적의 해를 보장하는 이유는
- 동전의 단위에서 가장 큰 단위가 작은 단위의 배수이므로(100원, 50원, 10원 전부 다 500원으로 나누어 떨어지기 때문에) 작은 단위의 동전들을 종합해도 다른 최적의 해가 나올 수 없기 때문이다.
- 하지만 400원이라는 배수가 아닌 동전이 있다고 가정하면, 800원을 거슬러 줘야할 때 500원 400원 100으로 거슬러 주는 문제에 그리디 알고리즘은 500원 1개와 100원 3개로 확인할 것이다. 하지만 최적의 해는 400원 2개로 최소 2개를 사용해 800원을 낼 수 있다.
- 이처럼 그리디 알고리즘은 언제나 최적의 답을 알려줄 순 없다. 그래서 최적의 해를 구해도 그 값이 최선의 값인지 확인을 해야 한다.
- 가장 큰 화폐부터 거슬러 주는 것이 최적의 해를 보장하는 이유는
- 그리디 알고리즘의 시간 복잡도는 화폐가 n이라고 했을 때 O(n)이다. 즉, 화폐의 종류만큼 반복을 수행한다면 답을 도출할 수 있다.
- 거슬러줘야 하는 금액과는 무관하고, 동전의 총 종류에만 영향을 받는다.
- 일반적인 상황에선 최적의 해를 보장할 수 없을 때가 많은데, 코딩테스트에선 그리디 알고리즘으로 푼다해도 그 안에서 최적의 해가 되는 상황을 추론할 수 있어야 풀리도록 출제한다고 한다.
매트로이드 이론(Matroid Theory)
- 그래프 이론과 관련된 알고리즘으로 알고리즘의 일반화된 형태이다.
- 매트로이드의 속성을 만족하는 문제들은 매트로이드의 구조를 통해 일반화될 수 있으며, 이를 통해 그리디 알고리즘을 적용할 수 있다.
- 예를 들어, 최소 신장 트리, 작업 스케줄링 문제, 독립 집합 문제 등 다양한 문제들이 매트로이드의 속성을 만족한다.
- 매트로이드는 두 가지 속성을 가진 구조인데
- 교환성 : 어떤 집합 A가 다른 집합 B보다 원소의 개수가 하나 적을 때, B의 어떤 원소 b가 A에 추가될 수 있어 A와 B의 원소 개수를 같게 만들 수 있다.
- 포함성 : 매트로이드의 모든 부분 집합은 매트로이드이다.
- 매트로이드라는 집합 내에서 임의로 원소들을 골라 만든 부분집합 역시 매트로이드의 속성을 만족한다는 의미이다.
- 예를 들면 {1, 2, 3}이라는 집합의 부분 집합에는 {1}, {2}, {3}, {1, 2}, {1, 3} 등이 있는데, 이걸 매트로이드의 포함성 속성에 따르면 모든 부분집합들은 교환성을 만족하는 독립 집합들로 이루어 져야 한다.
- 마트료시카에 대입해보면 된다. 인형을 뽀개도 안에 같은 인형이 있고 뽀개도 안에 같은 인형이 있다. 이처럼 큰 집합에서 작은 부분집합을 뽑아내도 그 부분집합 역시 매트로이드의 성질을 가지는 것이다.
분할 정복(Divide and Conquer)
- 큰 문제를 작게 분할하여 각각 해결하고, 그 결과를 도합해 전체 문제를 해결한다.
- 즉, 문제를 작게 분할한 후 각각을 정복하는 알고리즘이다.
- 작은 문제는 원래 문제와 같은 형태를 가지기 때문에, 원래 문제의 일부분이 된다.
- 그렇기 때문에 재귀적으로 반복해 해결하고 결합하여 원래 문제를 해결한다.
- 예시로는 이진 탐색, 합병 정렬, 퀵 정렬 등이 있다.
- 단계
- 분할 정복 알고리즘은 세 단계로 구성된다.
- 1. 분할 : 문제를 작은 문제로 분할
- 2. 정복 : 각 하위 문제는 재귀적으로 해결
- 3. 결합 : 하위 문제의 해결책을 결합하여 원래 문제를 해결
- 분할 정복 알고리즘은 세 단계로 구성된다.
- 장단점
- 장점
- 1. 빠른 속도
- 문제를 하위 문제들로 분할하고 해결하기 때문에 시간 단축이 된다.
- 2. 쉬운 병렬화
- 하위 문제를 병렬로 처리하기 쉬우므로 멀티코어 시스템에서 성능이 크게 향상된다.
- 3. 유연성
- 여러 응용 분야에서 사용될 수 있으며, 문제의 복잡도와 데이터 크기에 상관없이 적용할 수 있다.
- 1. 빠른 속도
- 단점
- 1. 추가적인 메모리 요구
- 재귀적으로 호출되기 때문에 많은 메모리를 필요로 할 수 있다.
- 2. 최악의 경우 시간 복잡도
- 일부 문제에 대해서는 최악의 경우의 시간 복잡도를 예측하기 어렵기 때문에 성능이 크게 달라질 수 있다.
- 예시
- 퀵 정렬은 분할 정복 알고리즘의 한 종류로, 피벗을 기준으로 분할해 정렬하는 방식이다. 하지만 피벗 설정이 잘못되면 균등하게 분할이 되지 않는데 그 때의 시간 복잡도는 O(n^2)가 된다.
- 3. 구현의 복잡성
- 구현이 비교적 복잡할 수 있으며, 종종 추가적인 문제를 발생시킬 수 있다.
- 1. 추가적인 메모리 요구
- 장점
- 예시
import sys
sys.setrecursionlimit(10**4)
def bunhal(start, end):
if start == end:
return start
mid = (start + end) // 2
return bunhal(start, mid) + bunhal(mid+1, end)
print(bunhal(1, 10))
print(bunhal(1, 100))
print(bunhal(1, 256))
print(bunhal(1, 317))
- 시작값부터 끝값까지 모두 더하는 로직에 분할정복을 이용해서 시작값부터 중간값까지, 중간값부터 끝값까지 병렬적으로 계산해 도합하는 방식이다.
- 이처럼 기존 작업을 분할하여 효율적으로 시간 단축을 줄이는 알고리즘이 분할 정복 알고리즘이다.
학습 시간 : 10 ~ 25시
728x90
'크래프톤 정글 > TIL' 카테고리의 다른 글
| 크래프톤 정글 week03, day20 - 어셈블리어, 오퍼랜드, 점프 인스트럭션, 프로시저 (1) | 2024.02.20 |
|---|---|
| 크래프톤 정글 week03, day19 - LCS 문자열 방식, 부분 수열 방식 (1) | 2024.02.20 |
| 크래프톤 정글 week02, day17 - 알고리즘 문제 (1) | 2024.02.20 |
| 크래프톤 정글 week02, day16 - 이론 공부, 알고리즘 문제 (1) | 2024.02.20 |
| 크래프톤 정글 week02, day15 - 힙(heap), 알고리즘 문제 (1) | 2024.02.20 |
