| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백준
- HTML
- 핀토스
- 크래프톤정글
- 소켓
- 자바스크립트
- 리액트
- corou
- Vue.js
- 크래프톤 정글
- 4기
- 큐
- CSS
- 알고리즘
- 자바
- Java
- 사이드프로젝트
- 프로그래머스
- 스택
- userprog
- 코드트리
- 정보처리기사
- pintos
- 나만무
- Flutter
- JavaScript
- defee
- TiL
- 시스템콜
- 모션비트
- Today
- Total
문미새 개발일지
깊이 우선 탐색(DFS, depth-first search), 너비 우선 탐색(BFS, Breadth-first search) 본문
깊이 우선 탐색(DFS, depth-first search), 너비 우선 탐색(BFS, Breadth-first search)
문미새 2024. 4. 2. 21:17깊이 우선 탐색(DFS, depth-first search)

깊이 우선 탐색(DFS)은 그래프의 모든 노드를 탐색하는데 사용되는 알고리즘 중 하나이다.
루트 노드에서 시작해 한 방향으로(주로 왼쪽부터) 들어갈 수 있는한 끝까지 탐색하여 더 이상 들어갈 수 없는 경우, 가장 최근의 분기점으로 돌아가 다른 방향의 노드를 탐색하는 방식으로 진행된다.
DFS의 구현
// 그래프를 인접 리스트 형태로 표현
const graph = {
A: ['B', 'C'],
B: ['A', 'D', 'E'],
C: ['A', 'F'],
D: ['B'],
E: ['B', 'F'],
F: ['C', 'E']
};
// DFS 함수 정의
function dfs(graph, startNode) {
let visited = []; // 방문한 노드를 체크하기 위한 배열
let stack = [startNode]; // 시작 노드 체크
// stack의 길이만큼 반복하며
while (stack.length !== 0) {
const node = stack.pop(); // 스택에서 노드 하나를 꺼내 저장
if (!visited.includes(node)) { // 해당 노드를 방문하지 않았다면
visited.push(node); // 방문한 노드 목록에 추가
const neighbors = graph[node]; // 인접 노드 목록
for (let neighbor of neighbors) {
if (!visited.includes(neighbor)) { // 인접 노드를 방문하지 않았다면
stack.push(neighbor); // 스택에 추가
}
}
}
}
return visited; // 방문한 노드 순서 반환
}
// 함수 실행 예시
console.log(dfs(graph, 'A')); // 예를 들어 'A' 노드에서 시작DFS는 스택이나 재귀를 이용해 구현할 수 있다. 위 코드에서는 스택을 사용해 구현되었으며, 방문하지 않은 노드 중 현재 노드와 인접한 노드를 스택에 추가하고, 스택에서 노드를 하나씩 꺼내 해당 노드를 현재 노드로 설정 후 과정을 계속 반복한다.
재귀 호출을 사용해 구현했을 때는, 현재 노드에 갈 수 있는 가능한 모든 방향으로 재귀탐색을 진행한다.
DFS를 사용하는 주요 이유 중 하나는 경로의 존재 여부를 판단하거나 모든 노드를 방문하기 위함이다. 또한 사이클의 존재 여부를 검사하거나 그래프의 연결 요소를 찾는 데 유용하다. 그리고 트리나 그래프의 깊이를 측정하는 데에도 사용될 수 있다.
DFS 특징
- 깊이 우선 : DFS는 현재 노드에서 더 이상 깊이 들어갈 수 없을 때까지 깊이 들어간 후, 다른 방향으로 탐색을 진행한다.
- 스택 or 재귀 사용 : DFS는 스택을 사용하거나 재귀 호출을 통해 구현할 수 있으며, 재귀 호출을 사용할 경우 시스템 스택이 사용되므로, 별도의 스택을 관리할 필요가 없다.
- 경로 탐색에 유용 : DFS는 모든 가능한 경로를 탐색하며, 특정 노드로부터 목표 노드까지의 경로를 찾는데 유용하다.
- 백트래킹(Backtracking)과의 연관성 : DFS는 백트래킹 기법의 기반이 되며, 해를 찾지 못했을 때, 이전 분기점으로 돌아가 다른 경로를 탐색하는 과정에 사용한다.
DFS의 시간 복잡도는 그래프의 표현 방식에 따라 다를 수 있지만, 일반적으로 노드 수 V, 간선 수 E라고 할 때, 인접 리스트로 표현된 그래프에서는 O(V + E), 인접 행렬로 표현된 그래프에서는 O(V ^ 2)이다.
너비 우선 탐색(BFS, Breadth-first search)
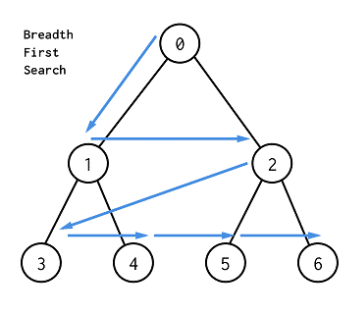
너비 우선 탐색(BFS)는 그래프의 모든 노드를 탐색하는 데 사용되는 알고리즘 중 하나이다.
시작 노드에서 시작해 가장 가까운 노드부터(해당 노드의 자식 노드) 쭉 탐색하며 DFS와 다르게 해당 레벨에 있는 노드를 다 탐색해 가는 방식으로 진행된다.
BFS의 구현
// 그래프를 인접 리스트 형태로 표현
const graph = {
A: ['B', 'C'],
B: ['A', 'D', 'E'],
C: ['A', 'F'],
D: ['B'],
E: ['B', 'F'],
F: ['C', 'E']
};
// BFS 함수 정의
function bfs(graph, startNode) {
let visited = []; // 방문한 노드를 기록하기 위한 배열
let queue = [startNode]; // 큐 초기화
// 큐에 노드가 있는 동안 반복
while (queue.length > 0) {
const node = queue.shift(); // 큐에서 노드를 하나 꺼냄
if (!visited.includes(node)) { // 해당 노드를 방문하지 않았다면
visited.push(node); // 방문한 노드 목록에 추가
const neighbors = graph[node]; // 인접 노드 목록
for (let neighbor of neighbors) {
if (!visited.includes(neighbor)) { // 인접 노드를 방문하지 않았다면
queue.push(neighbor); // 큐에 추가
}
}
}
}
return visited; // 방문한 노드 순서 반환
}
// 함수 실행 예시
console.log(bfs(graph, 'A')); // 예를 들어 'A' 노드에서 시작위 코드처럼 BFS는 큐를 사용해 구현된다. 탐색을 시작할 노드를 큐에 삽입하고 방문처리를 하며, 큐에서 노드를 하나 꺼내서 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리한다. 큐가 빌 때까지 계속 반복한다.
BFS 특징
- 단계별 탐색 : BFS는 시작 노드로부터 거리(단계)에 따라 탐색을 진행한다. 즉, 탐색하는 해당 노드에 인접한 노드(자식 노드)를 먼저 탐색하고, 그 다음에는 해당 노드에 인접한 노드들을 탐색하는 식으로 진행된다.
- 최단 경로 : BFS는 무게가 동일한 간선으로 구성된 그래프에서 시작 노드로부터 각 노드까지의 최단 경로를 찾을 때 사용할 수 있다.
- 큐 사용 : BFS 구현 시 큐를 사용하여 현재 탐색 중인 노드의 인접 노드들을 순차적으로 처리한다.
BFS의 시간 복잡도는 노드 수 V, 간선 수 E라고 할 때, 인접 리스트로 표현된 그래프에서는 O(V + E), 인접 행렬로 표현했을 때는 O(V ^ 2)가 된다.
'공부 키워드 > 알고리즘 및 데이터 구조' 카테고리의 다른 글
| 그래프(Graph) (1) | 2024.04.03 |
|---|---|
| 해시 테이블(Hash Table) (0) | 2024.04.01 |
| Deep Copy vs Shallow Copy (1) | 2024.03.31 |
| 스택(Stack), 큐(Queue) (3) | 2024.03.29 |
| 연결 리스트(Linked List) (1) | 2024.03.29 |



