728x90
위상정렬
- 수서가 정해져 있는 작업을 차례로 수행해야 할 때 그 순서를 결정해 주기 위해 사용하는 알고리즘
- 답이 한 가지가 아니라 여러 가지가 존재할 수 있고 DAG(Directed Acyclic Graph)에만 적용이 가능하다.
- DAG는 사이클이 발생하지 않는 방향 그래프이며, 사이클이 발생하면 위상정렬을 수행할 수 없다.
- 위상정렬은 두 가지 해결책을 낼 수 있는데
- 현재 그래프가 위상정렬이 가능한지, 위상정렬이 가능하면 그 결과는 무엇인지이고 스택과 큐를 이용해 알고리즘을 짤 수 있다.
- 진행 과정(큐를 사용)
- 1. 진입차수가 0인 정점을 큐에 삽입
- 2. 큐에서 원소를 꺼내 연결된 모든 간선 제거
- 3. 간선 제거 이후 진입차수가 0이 된 정점을 큐에 삽입
- 4. 큐가 빌 때 까지 2번, 3번 과정 반복.
- 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과이다.
- 과정 결과
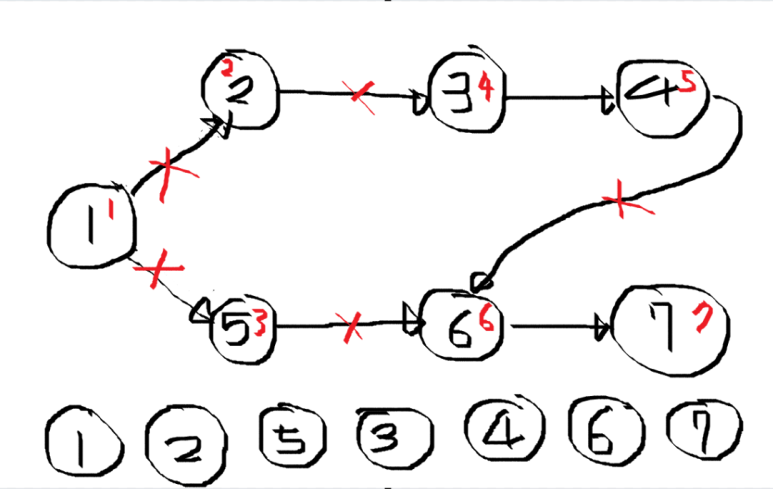
- 예시
- 대학에서 특정 전공을 이수하기 위해 수강해야 하는 과목과 선수과목이 있다고 가정할 때, 일부 과목들은 다른 과목들을 먼저 수강해야 한다.
- 그래프로 표현하면 각 과목은 정점이 되고 한 과목이 다른 과목의 선수과목이면 두 과목을 연결하는 화살표가 된다.
- 위상정렬을 이용해 과목들의 수강 순서를 찾을 수 있고, 결과는 선수 과목을 먼저 수강하고 다음 해당 과목을 수강하는, 과목들의 순서를 나타낸다.
- 이런식으로 모든 과목을 수강할 수 있는 순서를 찾을 수 있다.
트리(Tree)
계층적인 구조를 표현할 때 사용할 수 있는 자료구조
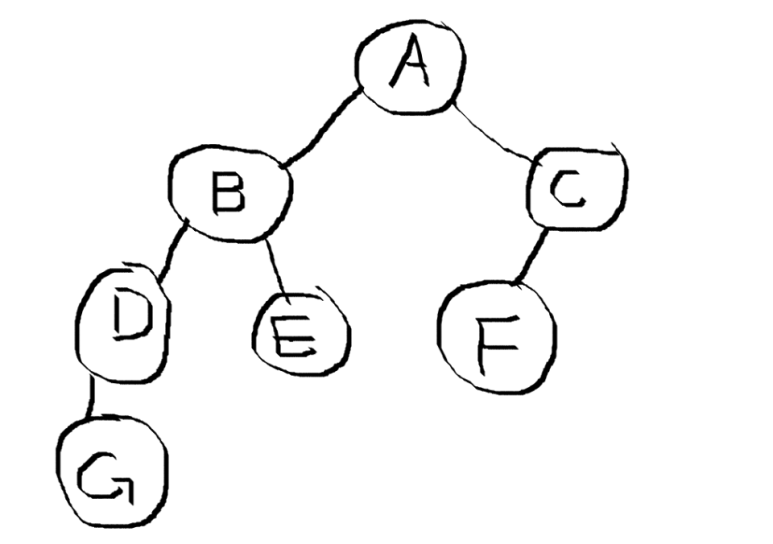
- 용어
- 루트 노드(root node) : 부모가 없는 최상위 노드
- 단말 노드(leaf node) : 자식이 없는 노드
- 크기(size) : 트리에 포함된 모든 노드의 개수
- 깊이(depth) : 루트 노드부터의 거리
- 높이(height) : 깊이 중 최댓값
- 차수(degree) : 각 노드의 간선 개수
- 기본적으로 트리의 크기가 N일 때, 전체 간선의 개수는 N-1개이다.
비트리
- B트리는 이진트리에서 발전해 모든 리프노드들이 같은 레벨을 가질 수 있도록 자동으로 밸런스를 맞추는 트리이다.
- 이진트리와 다르게 하나의 노드에 많은 수의 정보를 가지고 있을 수 있어, 최대 M개의 자식을 가질 수 있는 B트리를 M차 B트리라고 한다
- 특징
- 노드는 최대 M개부터 M/2개 까지의 자식을 가질 수 있다.
- 노드에는 최대 M-1개부터 [M/2]-1개의 키가 포함될 수 있다.
- 노드의 키가 x개라면 자식의 수는 x + 1개 이다.
- 최소 차수는 자식수의 하한값을 의미하며, 최소차수가 t라면 M = 2t - 1을 만족
- 최소차수 t가 2라면 3차 B트리이며, key의 하한은 1개이다.
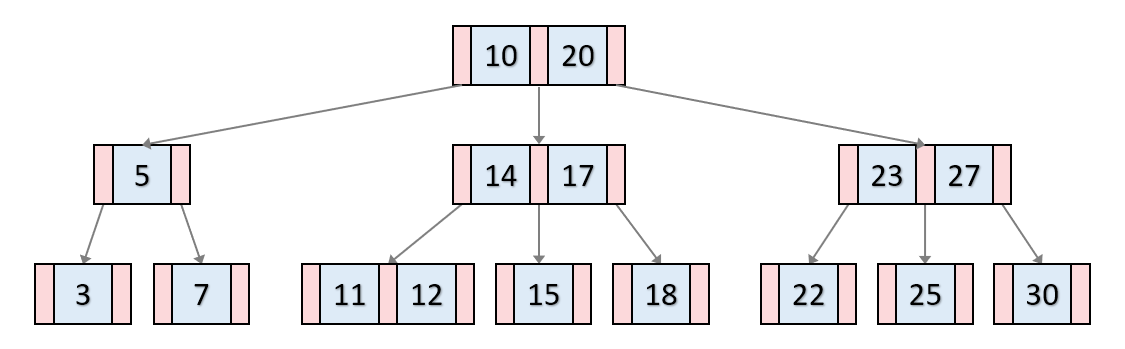
- 위 그림은 차수가 3인 B트리 이며 파란색 부분은 각 노드의 key를, 빨간색 부분은 자식 노드들을 가리키는 포인터이다.
- key들은 노드 안에서 항상 정렬된 값을 가지며, 이진검색트리처럼 각 key들의 왼쪽 자식들은 항상 key보다 작은 값을, 오른쪽은 큰 값을 가지는 탐색 트리이다.
- 데이터 삽입
- 추가는 항상 leaf 노드에 한다.
- 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.
- 노드가 넘친다는 말은 M차 B트리에서 각 노드는 최대 M-1개의 key를 가지게 되는데, 데이터를 삽입하는 과정에서 이를 위반한 것이다.
- 삽입 과정
- 1. 트리가 비어있다면 루트 노드를 할당하고 k를 삽입
- 2. 트리가 비어있지 않다면, 데이터를 넣을 적절한 리프 노드 생성
- 3. 리프노드에 데이터를 넣고 리프노드가 적절한 상태에 있다면 종료
- 4. 리프노드가 부적절한 상태에 있다면 분리한다.
- 분할이 일어나지 않았을 경우, 리프노드가 넘치지 않았다면 오름차순으로 k를 삽입한다.
- 분할이 일어났을 경우, 리프노드에 key노드가 가득 찼을 때 노드를 분할해야 한다.
- 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.
- B트리 데이터 삭제
- 삭제도 항상 leaf노드에서 발생하며, 삭제 후 최소 key 수 보다 적어지면 재조정한다.
- 각 노드는 최소 [M/2]-1개의 키를 가진다. (루트 노드 제외)
- 삭제도 항상 leaf노드에서 발생하며, 삭제 후 최소 key 수 보다 적어지면 재조정한다.
트라이(Trie)
- 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조이다.
- 기수 트리(radix tree), 접두사 트리(prefix tree), 탐색 트리(retrieval tree)라고도 한다.
- 검색할 때 볼 수 있는 자동완성 기능이나 사전 검색 등, 문자열을 탐색하는데 특화되어 있는 자료구조이다.
- 탐색을 할 때 위 그림 처럼 한 글자씩 찾아 들어가는 방식이다.
- 장점
- 문자열을 탐색할 때 빠르기 때문에, 하나하나씩 전부 비교하면서 탐색하는 것 보다 시간 복잡도 측면에서 훨씬 효율적이다.
- 단점
- 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있기 때문에 저장 공간의 크기가 크다.
- 즉, 메모리 측면에서 비효율적일 수 있음
- 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있기 때문에 저장 공간의 크기가 크다.
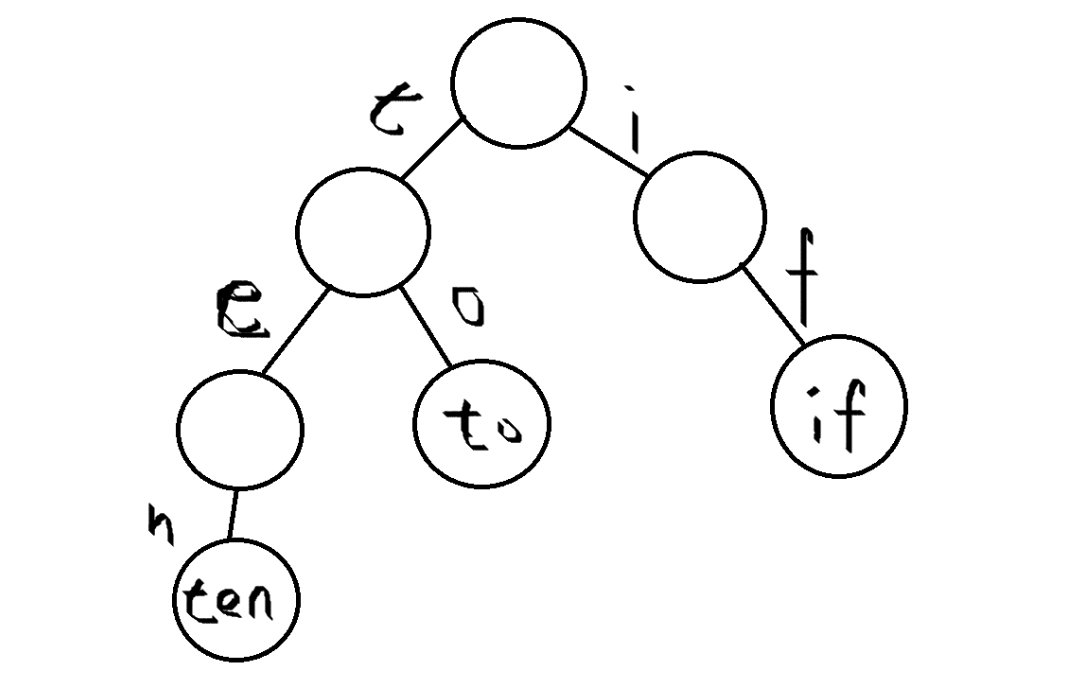
- 과정
1. ten 입력하기
- 1. 첫 번째 문자는 t이고 자료구조 내에 아무것도 없기 때문에 head의 자식 노드에 t를 추가
- 2. t 노드에 자식이 없으므로, t의 자식노드에 e를 추가
- 3. e도 마찬가지로 자식 노드 n을 추가한다.
- 4. n에 자식이 없어 단어가 끝이므로 노드에 ten을 표시
2. to 입력하기
- 1. 이미 head의 자식노드 t가 존재해서 추가하지 않고, t로 이동한다.
- 2. 자식노드가 하나 더 있어 o를 추가하고 단어가 끝이므로 노드에 to를 표시
3. if 입력하기
- 1. head의 자식노드로 t만 존재하고 i는 없기 때문에 자식노드에 i를 추가한다.
- 2. i의 자식노드가 없어 f를 추가한다.
- 단어가 f에서 끝이므로 현재 노드에 if를 표시한다.
- 제일 긴 문자열 길이를 L, 총 문자열들의 수를 M이라 할 때 트라이의 생성 시간 복잡도는 O(MxL), 탐색 시간 복잡도는 O(L)이다.
- 생성 시간 복잡도는 모든 문자열 M개를 넣어야 하고, M개에 대해 트라이에 넣는 건 L만큼 걸리므로 O(MxL)의 시간 복잡도를 가진다.(삽입은 O(L))
- 탐색 시간 복잡도는 트리를 제일 깊게 탐색할 때 L까지 깊게 들어가므로 O(L)의 시간 복잡도를 가짐.
최소 신장 트리(Minimum Spanning Tree)
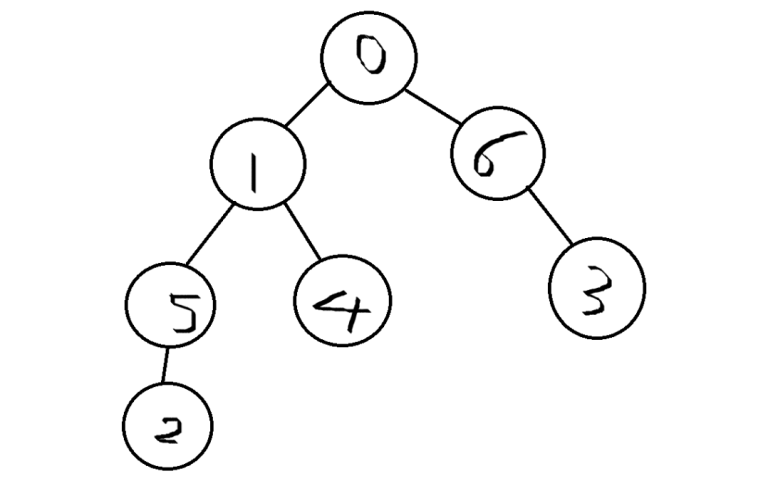
- 신장 트리는 그래프 내에 있는 모든 정점을 연결하고 사이클이 없는 그래프를 의미한다.
- n개의 정점이 있다면 신장 트리의 간선 수는 n-1개가 되고, 최소신장트리는 각 간선이 가지고 있는 가중치의 합이 최소가 되는 신장 트리이다.
- 가중치는 거리, 비용, 시간 등 여러가지로 운용이 가능하다.
- 최소신장트리의 대표적인 알고리즘은 프림 알고리즘과 크루스칼 알고리즘이 있다.
- 프림 알고리즘(Prim's Algorithm)
- 로버트 프림이 만든 최소신장트리 알고리즘이며, 정점 주변에 있는 간선의 가중치 중 가장 작은 것을 골라 최소 신장 트리를 만드는 방법이다.
- 과정
- 1. 그래프와 비어있는 최소신장트리를 만듦
- 2. 임의의 정점을 시작 정점으로 선택하고 최소신장트리의 루트 노드로 삽입
- 3 최소신장트리에 삽입된 정점과 인접한 정점의 가중치를 확인해서 가장 작은 가중치를 최소신장트리에 삽입
- 4. 3번 과정 반복 후 모든 정점이 최소신장트리에 연결되면 종료
- 프림 알고리즘에서 문제가 되는 건 최소 가중치를 찾는 것이다. 그래프에 N개의 정점이 있으면, N개의 정점을 추가하고, N개의 정점을 순회해야 하므로 최소 가중치를 찾기 위해선 NxN = N^2를 반복해야 한다.
- 크루스칼 알고리즘(Kruskal's Algorithm)
- 그래프 내의 모든 간선의 가중치를 확인하고 가장 작은 가중치부터 확인해 최소신장트리를 만드는 방법이며, 크루스칼 알고리즘은 탐욕적인(Greedy) 방법을 사용한다.
- 과정
- 1. 그래프 내의 모든 간선의 가중치를 오름차순으로 정렬
- 2. 오름차순으로 정렬된 가중치를 순회하며 최소신장트리에 삽입
- 크루스칼 알고리즘에선 사이클을 확인하기 위해 분리 집합(Disjoint Set)을 사용하며, 분리 집합은 공통된 원소를 갖지 않는 집합을 의미한다.
학습시간 : 10 ~ 25시
728x90
'크래프톤 정글 > TIL' 카테고리의 다른 글
| 크래프톤 정글 week02, day14 - sys, 람다, 유니온-파인드, 알고리즘 문제 (2) | 2024.02.19 |
|---|---|
| 크래프톤 정글 week02, day13 - 트리, 알고리즘 문제 (1) | 2024.02.19 |
| 크래프톤 정글 week02, day11 - 그래프 (1) | 2024.02.19 |
| 크래프톤 정글 week01, day10 - 알고리즘 문제 (1) | 2024.02.19 |
| 크래프톤 정글 week01, day09 - 알고리즘 문제 (1) | 2024.02.19 |
