728x90
힙 정렬(Heap Sort)
- 힙(Heap)은 완전 이진 트리(Complete Binary Tree)의 일종으로, 부모 노드와 자식 노드 간에 특정한 조건을 만족하는 자료구조를 말한다.
- 여기서 완전 이진 트리란 부모 노드 밑에 자식 노드가 최대 2개까지 있을 수 있고, 마지막 레벨을 제외한 모든 레벨에 노드가 완전히 채워져 있는 트리 구조를 말한다.
- 힙은 우선순위 큐를 위해서 만들어진 자료구조이며, 특히 힙은 부모 노드와 자식 노드 간의 관계를 통해 정의된다.
- 자식 노드가 있는 노드는 항상 (원소의 개수 / 2) 이다.
- 종류
- 최대 힙(Max Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 크거나 같은 값을 가진 완전 이진 트리이다
- 최댓값을 빠르게 찾아내는 데 사용된다.
- 최소 힙(Min Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작거나 같은 값을 가진 완전 이진 트리이다.
- 최솟값을 빠르게 찾아내는데 사용된다.
- 최대 힙(Max Heap)
- 최대 힙 설명
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
6
|
4
|
8
|
2
|
5
|
10
|
9
|
1
|
3
|
7
|

- 최대 힙은 항상 부모가 자식보다 크거나 같기 때문에 자식을 가지고 있는 부모 노드와 그 자식 노드와 비교하면 된다.
- 자식을 가진 부모 노드는 4번 인덱스까지 있기 때문에 4번부터 순서대로 올라가며 비교를 한다.
- 자식을 가지고 있는 노드는 6, 4, 8, 2, 5이다. 이 노드를 자식 노드와 비교해서 부모가 더 크게 바꿔야 한다.
1. 4번 인덱스인 5와 자식 노드 7을 비교해서 7이 더 크기 때문에 자식이 위로 올라온다. 그리고 배열에 있는 값도 교체를 해준다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
6
|
4
|
8
|
2
|
7
|
10
|
9
|
1
|
3
|
5
|
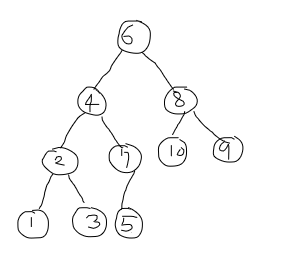
2. 3번 인덱스인 2와 자식 노드 3을 비교해서 3이 더 크기 때문에 자식이 위로 올라온다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
6
|
4
|
8
|
3
|
7
|
10
|
9
|
1
|
2
|
5
|
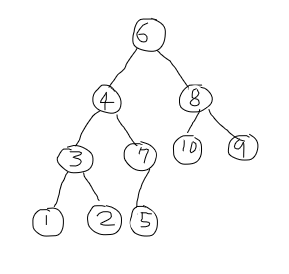
3. 2번 인덱스인 8과 자식 노드 10 9 중 더 큰 값인 10을 비교해서 10이 더 크기 때문에 자식이 위로 올라온다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
6
|
4
|
10
|
3
|
7
|
8
|
9
|
1
|
2
|
5
|
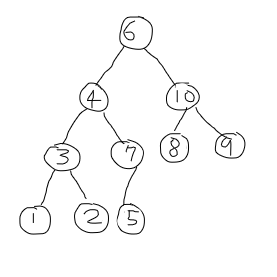
4. 1번 인덱스인 4와 자식 3과 7 중 더 큰 7을 비교해서 7이 더 크기 때문에 자식이 위로 올라온다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
6
|
7
|
10
|
3
|
4
|
8
|
9
|
1
|
2
|
5
|

5. 하지만 교환을 했을때 부모 노드 4보다 자식노드 5가 더 크기 때문에 이 값도 변경을 해줘야 한다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
6
|
7
|
10
|
3
|
5
|
8
|
9
|
1
|
2
|
4
|

6. 0번 인덱스인 6과 7과 10 중 더 큰 10을 비교해서 10이 더 크기 때문에 자식이 위로 올라온다. 그리고 바뀐 6도 자식 노드인 8과 9를 비교해 더 큰 9가 6보다 크기 때문에 6과 9를 변경해준다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
10
|
7
|
9
|
3
|
5
|
8
|
6
|
1
|
2
|
4
|

7. 이러면 max 힙 정렬이 완료된 것이다.
- 힙 정렬을 하려면 배열을 heapify를 시켜줘야 한다.
- heapify
- 주어진 데이터를 힙 구조로 만드는 과정을 의미한다.
- 이 과정은 특정 노드를 루트로 하는 서브 트리가 힙 성질을 유지하도록 하여, 전체 트리가 힙이 되게 한다.
- heapify
- 정렬이 완료되면 가장 큰 값이 0번 인덱스로 오게 되는데, 이 때 0번 인덱스 값과 마지막 인덱스 값을 교환한다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
4
|
7
|
9
|
3
|
5
|
8
|
6
|
1
|
2
|
10
|

- 이제 가장 마지막 인덱스 값은 정렬이 완료됐기 때문에 제외하고 다음 정렬을 진행하는데, 현재 0번 인덱스에 4번이 와 있지만 자식 노드 중에 4보다 더 큰 값이 있기 때문에 정렬된 10번을 제외하고 다시 heapify를 진행해줘야 한다.
- 같은 방식으로 끝까지 진행한다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
9
|
7
|
8
|
3
|
5
|
4
|
6
|
1
|
2
|
10
|

- 이러면 또 0번 인덱스에 남은 값 중 가장 큰 값이 들어가기 때문에 이 방식을 계속 반복해서 heapify를 해줘야 한다.
|
index
|
[0]
|
[1]
|
[2]
|
[3]
|
[4]
|
[5]
|
[6]
|
[7]
|
[8]
|
[9]
|
|
node
|
2
|
7
|
8
|
3
|
5
|
4
|
6
|
1
|
9
|
10
|

- 이런 식으로 정렬이 완료되면 힙 정렬이 완성된다.

- 전부 돌면서 정렬을 맞추기 때문에 heapify의 시간복잡도는 O(logN)이 걸린다.
- 그리고 총 데이터의 개수는 N이기 때문에 힙정렬의 시간복잡도는 O(NlogN)이 걸린다.
// 배열을 힙으로 바꾸기 위해 정렬하는 히피파이
def heapify(unsorted, index, heap_size):
// 가장 큰 값에 현재 부모값 넣기
largest = index
// 현재 부모 * 2 + 1하면 왼쪽 자식 인덱스가 나온다.
left_index = 2 * index + 1
// 현재 부모 * 2 + 2하면 오른 자식 인덱스가 나온다.
right_index = 2 * index + 2
// 만약 배열을 벗어나지 않고 왼쪽 자식이 부모보다 크면
if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
// 부모 값에 왼쪽 자식값 넣기
largest = left_index
// 만약 배열을 벗어나지 않고 오른쪽 자식이 부모보다 크면
if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
// 부모 값에 오른쪽 자식값 넣기
largest = right_index
// 위에서 인덱스만 바꾼거라 값도 바꿔주기 위함
if largest != index:
// 부모값과 자식값을 교환
unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
// 자식으로 내려간 값의 자식들이랑 비교하기 위해 한번더 히피파이 진입
heapify(unsorted, largest, heap_size)
// 힙정렬 함수
def heap_sort(unsorted):
// 인자로 받아온 배열의 길이를 n에 담기
n = len(unsorted)
// 부모노드의 개수는 전체 노드의 절반 -1이기 때문에 부모 노드를 밑에서 부터 시작
// -1씩 내려가면서 부모노드를 탐색하며
for i in range(n // 2 - 1, -1, -1):
// 배열과 탐색할 부모노드, 배열 길이를 인자로 히피파이 진입
heapify(unsorted, i, n)
// 히피파이가 완료됐으면 맨 앞 인덱스와 맨 뒤 인덱스를 바꿔주기 위함
for i in range(n - 1, 0, -1):
// 맨 앞 맨 뒤를 바꿔주고 맨 뒤값은 정렬이 되었기 때문에
unsorted[0], unsorted[i] = unsorted[i], unsorted[0]
// 빼고 다시 히피파이 진입
heapify(unsorted, 0, i)
// 그리고 배열 반환
return unsorted
if __name__ == "__main__":
// 힙 정렬 하기 전의 배열 입력 받기
unsorted = [3,18,7,5,1,9,14,28]
// 배열을 힙정렬 함수로 보내 리턴 값을 출력
print(heap_sort(unsorted))
학습 시간 : 10 ~ 25시
728x90
'크래프톤 정글 > TIL' 카테고리의 다른 글
| 크래프톤 정글 week05, day45 - Malloc Lab(Implicit), 잔디심기 (1) | 2024.02.22 |
|---|---|
| 크래프톤 정글 week05, day44 - 퀴즈, 메모리 관리 전략, 잔디심기 (2) | 2024.02.21 |
| 크래프톤 정글 week05, day42 - 메모리 관련 키워드 (2) | 2024.02.21 |
| 크래프톤 정글 week05, day41 - 시스템 콜 함수, IPC (1) | 2024.02.21 |
| 크래프톤 정글 week05, day40 - 예외적인 제어 흐름 (1) | 2024.02.21 |

