728x90
시간 복잡도(Time Complexity)
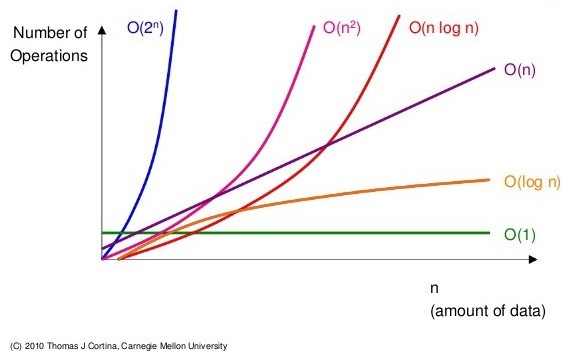
알고리즘을 실행하는데 필요한 시간이 입력의 크기에 따라 어떻게 변화하는지를 나타내는 척도이다.
이는 알고리즘의 효율성을 평가하는 중요한 기준 중 하나로, 알고리즘의 실행 시간이 입력 크기에 따라 얼마나 증가하는지를 분석함으로써, 알고리즘을 이해하고 최적화하는데 도움이 된다.
시간 복잡도의 표현
시간 복잡도는 주로 빅오 표기법(Big O notation)을 사용하여 표현된다. 빅오 표기법은 최악의 경우 시간 복잡도를 나타내는데 사용되며, 알고리즘의 상한을 설명해준다.
예를 들어 O(n)은 알고리즘의 실행 시간이 입력 크기 n에 선형적으로 비례한다는 것을 의미한다.
주요 시간 복잡도
| 시간 복잡도 | 설명 | 예시 |
| O(1) | 상수 시간 | 입력 크기와 상관없이 실행 시간이 일정하다. ex) 배열에서 요소에 접근하기 |
| O(log n) | 로그 시간 | 입력 크기가 커질 수록 실행 시간이 로그 증가한다. ex) 이진 검색 |
| O(n) | 선형 시간 | 실행 시간이 입력 크기에 비례한다. ex) 선형 검색, 배열의 모든 요소 순회 |
| O(n log n) | 선형 로그 시간 | 많은 효율적인 정렬 알고리즘들이 이 시간 복잡도를 가진다. ex) 병합 정렬, 퀵 정렬, 힙 정렬 |
| O(n^2) | 제곱 시간 | 실행 시간이 입력 크기의 제곱에 비례한다. ex) 버블 정렬, 선택 정렬, 삽입 정렬 |
| O(n^3) | 세제곱 시간 | 실행 시간이 입력 크기의 세제곱에 비례한다. ex) 행렬의 곱셈 (기본 알고리즘) |
| O(2^n) | 지수 시간 | 실행 시간이 입력 크기의 지수 함수로 증가한다. ex) 피보나치 수열의 재귀적 계산, 부분 집합의 모든 조합 찾기 |
| O(n!) | 팩토리얼 시간 | 실행 시간이 입력 크기의 팩토리얼에 비례한다. ex) 외판원 문제 브루트 포스 해결, 모든 순열 생성 |
시간 복잡도의 중요성
- 효율성 분석 : 알고리즘의 효율성을 이해하고, 더 나은 알고리즘을 선택하거나 개발할 수 있다.
- 성능 예측 : 알고리즘의 실행 시간을 예측하여, 시스템의 성능 요구 사항을 충족시킬 수 있다.
- 자원 관리 : 알고리즘의 시간 복잡도를 통해, 필요한 컴퓨팅 자원을 더 잘 관리하고 할당할 수 있다.
알고리즘을 설계하거나 선택할 때는 시간 복잡도 뿐만 아니라 공간 복잡도(알고리즘이 사용하는 메모리 양)도 고려해야 한다. 최적의 솔루션을 위해서는 두 복잡도 사이의 균형을 찾아야 한다.
728x90
'공부 키워드 > 알고리즘 및 데이터 구조' 카테고리의 다른 글
| 스택(Stack), 큐(Queue) (3) | 2024.03.29 |
|---|---|
| 연결 리스트(Linked List) (1) | 2024.03.29 |
| 정렬 알고리즘 (3) | 2024.03.27 |
| 반복문과 재귀함수 (1) | 2024.03.27 |
| 배열과 문자열 (2) | 2024.03.26 |


